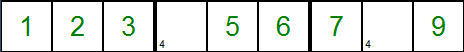IdentifiantMot de passe
Mot de passe oublié ?Je m'inscris ! (gratuit)

Sudoku Solver

Date de publication : 11 juin 2009 , Date de mise à jour : 24 Janvier 2010

Par Franck SORIANO
 

Le 5ème défi Delphi est terminé. Il s'agissait de réaliser un solveur pour grille de Sudoku.
J'ai profité de l'occasion pour en faire un exercice d'optimisation en Delphi. Dans cet article, je décris ma solution pour résoudre une grille de Sudoku, en détaillant toutes les étapes et la démarche suivie afin d'optimiser au mieux le résultat.
Venez commenter cet article directement sur le 505 commentaires Donner une note à l´article (5)

               Version PDF (Miroir)   Version hors-ligne (Miroir)

I. Analyse et Modélisation du problème
I-A. Analyse du problème
I-B. Algorithme naïf de résolution d'une grille
I-C. Définition des structures de données
I-D. Définition des méthodes de résolution
I-D-1. RechercherTousLesCandidats
I-D-2. RechercherMinimumCandidat
I-D-3. Resoudre
II. Optimisation de l'algorithme
II-A. La démarche générale
II-B. Optimisation de l'algorithme naïf 0
II-B-1. RechercherTousLesCandidats
II-C. Optimisation de l'algorithme naïf 1
II-D. Optimisation de l'algorithme naïf 2
II-D-1. RechercherMinimumCandidat
III. Optimisations techniques
III-A. Algorithme optimisé 0
III-B. Algorithme optimisé 1
III-C. Algorithme optimisé 2
III-D. Algorithme optimisé 3
III-E. Algorithme optimisé 4
III-F. Algorithme optimisé 5
III-G. Algorithme optimisé 6
III-H. Algorithme optimisé 7
IV. Algorithme final
V. Conclusion


I. Analyse et Modélisation du problème


I-A. Analyse du problème

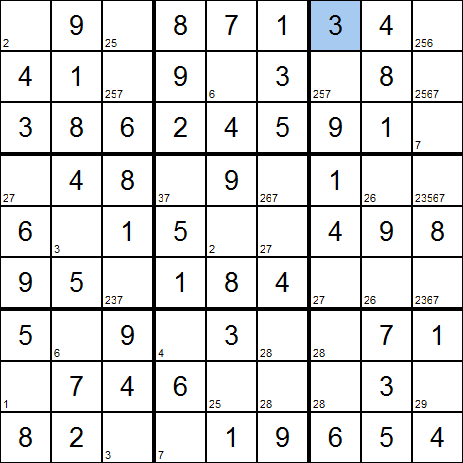
Commençons par étudier un peu les concepts du Sudoku. Nous commençons tout naturellement par la grille elle-même :

Une grille est un carré de 9x9, divisé en 9 régions de 3x3.

La grille est définie au départ avec un nombre de cellules pré-remplies. C'est ce qu'on appelle les révélés. Les révélés sont figés et le joueur ne peut pas les modifier. Il est d'usage de les afficher en noir.

Lorsqu'un joueur essaie de résoudre la grille manuellement, il va s'aider en définissant des petites notes dans chaque cellule. Il s'agit des candidats possibles pour la cellule en question.

Enfin, un joueur peut remplir une cellule avec une valeur lorsqu'il pense avoir trouvé un élément de solution. Si on joue la grille à la main, il serait bon de pouvoir distinguer les valeurs définies par le joueur des révélés. Ainsi, il faudrait qu'on puisse savoir si une valeur est un révélé ou valeur définie par le joueur.

Les révélés ne peuvent pas être modifiées par le joueur. En revanche, le joueur peut modifier une valeur d'une cellule qu'il a lui-même préalablement défini, du moment que les règles du Sudoku sont respectées :

  • Un chiffre ne peut apparaitre qu'une seule fois sur une ligne.
  • Un chiffre ne peut apparaitre qu'une seule fois sur une colonne.
  • Un chiffre ne peut apparaitre qu'une seule fois dans une région.

I-B. Algorithme naïf de résolution d'une grille

Essayons de réfléchir un instant à une méthode permettant de résoudre une grille. Bien sûr, on pourrait commencer par faire une recherche sur Internet, afin de trouver des méthodes de résolution existantes. Cependant, ça ne serait pas marrant. Essayons plutôt de trouver une méthode par nous même.

Pour cela, essayons de résoudre une grille à la main, et analysons notre démarche :

  • Face à une nouvelle grille, on va commencer par regarder cellule par cellule, quels sont les candidats possibles. On va ainsi annoter chaque cellule avec la liste des candidats, en se contentant d'appliquer strictement les règles du Sudoku.
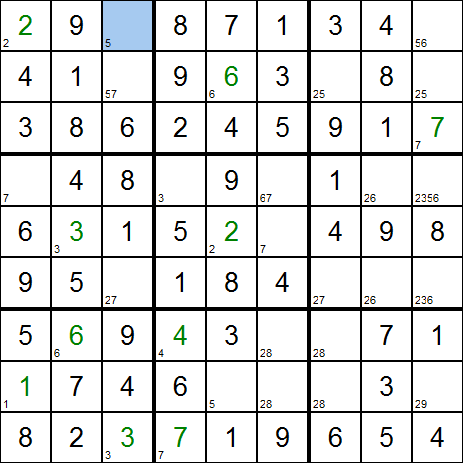
  • Dans l'exemple précédent, on se rend compte qu'il y a un certain nombre de cellules qui ne peuvent accepter qu'une seule et unique valeur. On peut donc être certain que la solution finale contiendra cette valeur dans cette case. On peut alors remplir systématiquement les cellules avec une seule solution, sans risque de se tromper.
  • Evidemment, en remplissant certaines cellules, on définit de nouvelles contraintes. Les candidats qui ont été définis lors des étapes précédentes ne sont plus valides, et il faut recommencer la recherche des candidats possibles pour chaque cellule vide.
On arrive alors au résultat suivant :

On constate qu'en remplissant certaines cellules, on a fait apparaître de nouvelles cellules avec un seul candidat possible. On peut donc continuer la résolution en répétant les mêmes opérations en boucle.

En fait, on s'aperçoit vite que toutes les grilles de niveau Très facile et Facile se résolvent uniquement de cette manière !

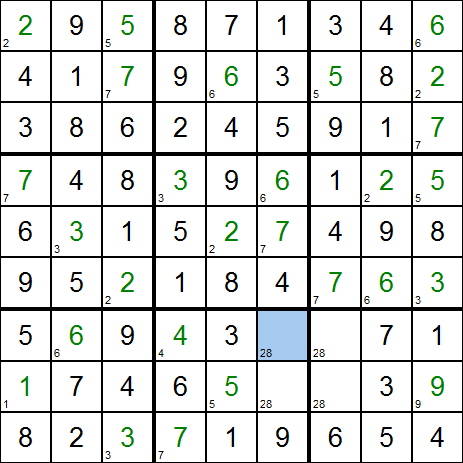
Cependant, lorsqu'on attaque des grilles un peu plus complexes, on finit par arriver dans une configuration où il n'y a aucune cellule certaine.

C'est finalement le cas ici :

Arrivé dans cette situation, on n'a pas vraiment le choix. On doit prendre une des cellules restantes (de préférence celle avec le moins de candidats possibles), essayer de remplir la cellule avec une des valeurs possibles et continuer la résolution en appliquant les mêmes méthodes que précédemment.

Deux cas de figure peuvent alors se présenter :

  • Soit on arrive à remplir complètement la grille : Dans ce cas, on a trouvé une solution au problème.
  • Soit on arrive dans une configuration où une cellule ne possède aucun candidat possible : Dans ce cas, le problème n'a pas de solution, ce qui signifie probablement qu'on a fait un mauvais choix à un moment et qu'il faut revenir en arrière jusqu'au dernier choix effectué, pour choisir une autre solution.
En fait, si on réfléchit un peu, on se rend compte qu'à chaque étape, on recherche les candidats possibles, puis on prend la cellule qui possède le moins de candidats et on essaie de remplir la cellule avec chacune de ses valeurs. En réalité, le cas où une cellule ne possède qu'un seul candidat n'est rien d'autre qu'un cas particulier.

Ainsi l'algorithme de résolution est le suivant : 

Résoudre grille (n)
Debut
  Rechercher tous les candidats
  Rechercher la première cellule qui possède le moins de candidats possibles
  Si toutes les cellules sont remplies
  Alors La résolution est terminée avec succès
  Sinon 
    Si on a trouvé une cellule avec aucun candidat
    Alors la grille n'a pas de solution
    Sinon 
      Pour chaque candidat de la cellule trouvée
      Debut
        remplir la cellule avec le candidat
        Résoudre la grille (N+1)
      Fin pour
    Fin si
  Fin si
Fin
Finalement, on a un algorithme récursif, très simple à comprendre et qui va nous permettre de résoudre n'importe quelle grille puisque tous les cas de figure sont traités. A chaque niveau de récursion on remplit une cellule de la grille, donc la résolution avance. La profondeur maximale de récursion sera de 81 (le nombre de cellules vides dans la grille),

La récursion se termine lorsque toutes les cellules sont remplies (le problème est résolu) ou lorsqu'il existe au moins une cellule qui n'a pas de solution (la grille ne peut plus être résolue).

C'est à présent, ce que nous allons réaliser. Nous verrons ensuite comment l'optimiser pour obtenir de bonnes performances.

Mais commençons d'abord par coder une solution simple et fonctionnelle !


I-C. Définition des structures de données

Si on veut modéliser une grille de Sudoku, on doit définir une structure de données qui puisse représenter tous les éléments vu précédemment.

Le plus simple dans un premier temps, serait de définir un tableau de 9x9 composés de cellule. Par exemple : 

FGrille : array[0..8, 0..8] of TCellule;
Avec : 

type
  TCellule = record
    Valeur : integer;    // Valeur de la cellule
    IsRevelee : boolean; // indique si la cellule est revélée : Sa valeur est fournie au départ.
    FlgCandidats : array[1..9] of boolean; // désigne les marques définies par le joueur
  end;
  PCellule = ^TCellule;
A présent, on peut généraliser un peu cette structure, et définir des constantes à la place des valeurs en dur. Ca donne le résultat suivant : 

const
  LGBLOC = 3;
  HTBLOC = 3;
  LARGEUR = LGBLOC*LGBLOC; // Largeur d'une grille de Sudoku
  HAUTEUR = HTBLOC*HTBLOC; // Hauteur d'une grille de Sudoku
  VALEUR_MIN = 1; // Plus petite valeur jouable
  VALEUR_MAX = LGBLOC*HTBLOC; // Plus grande valeur jouable.
  CELLULE_VIDE = 0; // Valeur d'une case vide.

type
  TCellule = record
    Valeur : integer;     // Valeur de la cellule
    IsRevelee : boolean; // indique si la cellule est revéllée : Sa valeur est fournie au départ.
    FlgCandidats : array[VALEUR_MIN..VALEUR_MAX] of boolean; // désigne les marques définies par le joueur
  end;
  TGrille = array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
On a ainsi tous les éléments nécessaires pour définir une grille de Sudoku à un instant donné.

Evidemment, on va définir tout ça à l'intérieur d'un objet.


I-D. Définition des méthodes de résolution

Reprenons à présent l'algorithme de résolution et commençons à coder les différents éléments dont nous avons besoin.


I-D-1. RechercherTousLesCandidats

Cette méthode doit analyser la grille pour trouver les candidats possibles des cellules vides.

Là encore, nous allons commencer par une implémentation naïve : 

// Analyse la grille de jeu pour déterminer tous les coups possibles pour chaque cellule. Autrement
// dit, pour chaque cellule, on regarde quelles sont les valeurs candidates.
procedure TSudokuNaif0.RechercherTousLesCandidats;
var
  x, y : integer;
begin
  for x := 0 to LARGEUR-1 do
  begin
    for y := 0 to HAUTEUR-1 do
    begin
      if FGrille[x, y].Valeur<>CELLULE_VIDE
      then continue;

      CandidatsPossibles(x, y); // On recherche les coups possible de la cellule.
    end;
  end;
end;


// Calcule les candidats possibles pour la cellule <x,y>
procedure TSudokuNaif0.CandidatsPossibles(x, y : integer);
var
  Candidat : integer;
  i,j : integer;
  x1, y1 : integer;
begin
  // Par défaut, tous les coups sont possibles.
  fillchar(FGrille[x, y].FlgCandidats, sizeof(FGrille[x, y].FlgCandidats), 1);

  // On essaie toutes les valeurs possibles et on regarde si chaque valeur est un candidat possible.
  for Candidat := VALEUR_MIN to VALEUR_MAX do
  begin
    // On regarde si la valeur n'est pas déjà utilisée sur le ligne.
    for i := 0 to LARGEUR-1 do
    begin
      if FGrille[i, y].Valeur = Candidat
      then FGrille[x, y].FlgCandidats[Candidat] := false; // Le candidat n'est pas possible !
    end;

    // On fait la même chose en colonne.
    for i := 0 to LARGEUR-1 do
    begin
      if FGrille[x, i].Valeur = Candidat
      then FGrille[x, y].FlgCandidats[Candidat] := false; // Le candidat n'est pas possible !
    end;

    // Et on recommence pour la région
    x1 := (x div LGBLOC)*LGBLOC;
    y1 := (y div HTBLOC)*HTBLOC;
    for i := x1 to x1 +LGBLOC-1 do
    begin
      for j := y1 to y1+HTBLOC-1 do
      begin
        if FGrille[i, j].Valeur = Candidat
        then FGrille[x, y].FlgCandidats[Candidat] := false; // Le candidat n'est pas possible !
      end;
    end;
  end;
end;

I-D-2. RechercherMinimumCandidat

La méthode RechercheMinimumCandidat doit retourner la première cellule vide qui possède le moins de candidats.

Elle doit effectuer la recherche, mais également nous dire si la grille est résolue ou si au contraire, il existe des cellules sans solution (au moins une, ça suffira).

En fait, il suffit de parcourir les cellules une par une et compter le nombre de candidats à chaque fois. Le nombre de candidat peut varier de 0 (grille impossible) à VALEUR_MAX-VALEUR_MIN+1. 

// Recherche la cellule qui possède le moins de candidats possible et retourne ses coordonnées
// dans <x, y>.
// La procédure peut renvoyer :
// <-1, -1> : Si toutes les cellules sont remplies.
// <-2, -2> : S'il existe une cellule avec aucun candidat possible.
procedure TSudokuNaif0.RechercherMinimumCandidat(var x, y: integer);
var
  i, j : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[VALEUR_MIN..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  for j := 0 to HAUTEUR-1 do
  begin
    for i := 0 to LARGEUR-1 do
    begin
      // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
      if FGrille[i, j].Valeur<>CELLULE_VIDE
      then continue;

      // A présent, on compte les candidats.
      nb := 0;
      for n := VALEUR_MIN to VALEUR_MAX do
      begin
        if (FGrille[i, j].FlgCandidats[n])
        then inc(nb);
      end;

      // Est-ce que la cellule possède au moin un candidat !
      if nb = 0
      then begin
        // La cellule n'a pas de solution. La grille est impossible !
        x := -2;
        y := -2;
        exit;
      end;

      if (nb > 0) and not CoupTrouve[nb]
      then begin
        // On vient de trouver la première cellule avec Nb candidats possibles.
        tbPossible[nb] := (i shl 8) or j;
        CoupTrouve[nb] := true;
      end;
    end;
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      x := (tbPossible[n] and $ff00) shr 8;
      y := tbpossible[n] and $ff;
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  x := -1;
  y := -1;
end;
info Vous remarquerez que j'ai utilisé les opérateurs shr et shl. Ces derniers permettent d'effectuer un décalage de bits vers la gauche (shl) ou vers la droite (shr). Chaque fois qu'on effectue un décalage vers la gauche, on multiplie la valeur décalée par 2. Ainsi, shl permet de multiplier rapidement une valeur par une puissance de deux, et shr fait l'opération inverse.
Le principal intérêt, c'est qu'un décalage est beaucoup plus rapide à calculer qu'une multiplication ou une division.
Dans le code précédent, j'utilise tbPossible pour stocker deux informations : Le numéro de ligne et le numéro de colonne. En fait, j'ai encodé les deux informations dans un seul entier. J'utilise un octet de poid fort pour la colonne, et l'octet de poids faible pour la ligne.
L'opération (i shl 8) or j, est en réalité équivalente à i*256+j.
A l'inverse, x := (tbPossible[n] and $ff00) shr 8 est équivalent à x := tbPossible[n] div 256.
y := tbpossible[n] and $ff est équivalent à y := tbpossible[n] mod 256.

I-D-3. Resoudre

Enfin, la méthode Resoudre va nous permettre de rechercher les solutions récursivement.

C'est la traduction directe de l'algorithme naïf présenté au début : 

// Tente de résoudre la grille depuis sa définition actuelle. En retour, la méthode renvoie :
// - true : La grille a été résolue avec succès !
// - false : La grille ne possède pas de solution !
function TSudokuNaif0.Resoudre(NbMaxSolution : integer) : boolean;
var
  x, y : integer;
  n : integer;
  old : array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
begin
  result := true;

  // On commence par rechercher les candidats des cellules vides.
  RechercherTousLesCandidats;

  // Puis on recherche la première cellule avec le moins de candidats
  RechercherMinimumCandidat(x, y);
  if (x=-1) and (y=-1)
  then begin
    result := true; // La résolution est terminée !
    MemoriserSolution; // On mémorise la solution trouvée.
  end
  else begin
    if (x=-2) and (y=-2)
    then result := false // La grille n'a pas de solutions !
    else begin
      // On commence par sauvegarder la grille en cas de retour arrière
      move(FGrille, old, sizeof(FGrille));

      // Puis on examine les candidats de la cellule
      for n := VALEUR_MIN to VALEUR_MAX do
      begin
        if FGrille[x, y].FlgCandidats[n]
        then begin
          // On essaie la résolution avec le candidat n
          FGrille[x, y].Valeur := n;

          // On continue recursivement.
          result := Resoudre(nbMaxSolution);

          // Si la grille a été résolue et qu'on a atteind le nombre maximum de solutions autorisé
          // on doit arrêter la recherche. Ca évite de boucler trop longtemps pour les grilles avec un
          // très grand nombre de solutions.
          if result and (ListeSolution.Count >= NbMaxSolution)
          then exit;

          // On vient de traiter le candidat n. On restaure la grille dans son état initial pour
          // continuer avec le candidat suivant.
          move(old, FGrille, sizeof(FGrille));
        end;
      end;
    end;
  end;
end;
Et voilà ! Le solveur naïf est terminé.

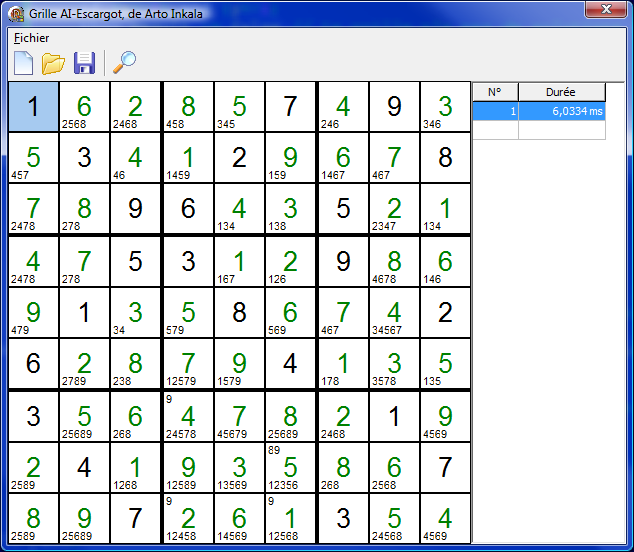
A présent, il ne reste plus qu'à l'essayer. Faisons un petit essai avec AI-Escargot (Algorithme naïf 0) :

La résolution se fait en 6 ms.

Cette solution a beau être un brouillon brut de fonderie, les performances sont déjà très bonnes !

On pourrait s'arrêter là. Mais puisqu'il s'agit d'un défi, autant essayer de l'optimiser un peu et voir si, après le brouillon on ne peut pas faire un chef d'œuvre !


II. Optimisation de l'algorithme


II-A. La démarche générale

Bien, à présent nous allons changer un peu de registre et nous lancer dans une démarche d'optimisation !

Optimiser, oui mais comment fait-on ? On pourrait prendre chaque ligne de code et voir comment grapiller quelque microsecondes à droite à gauche. On arrivera certainement à améliorer les temps de réponses. Cependant, une telle approche a toute les chances d'être assez peu rentable. En effet, on risque de passer beaucoup de temps à optimiser finement du code rarement exécuté, ou du code déjà très performant. Au final, le gain serait assez minime.

Il serait préférable de concentrer nos effort sur du code qui donnera tout de suite des résultats importants. Autrement dit, si on veut optimiser notre solution, on doit en premier lieu identifier son profil d'exécution. Il faut qu'on sache où se situent les goulots d'étranglement afin de se concentrer sur eux en priorité.

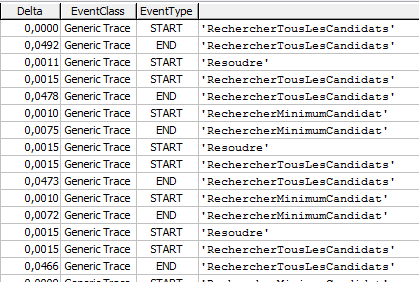
Pour cela, j'utilise Event Tracing for Windows (ETW) de façon à instrumenter le code : On ajoute un message au début et à la fin de chaque méthode. Ces messages seront écrits et horodatés en temps réel dans la trace. On pourra ainsi mesurer les temps d'exécution de chaque méthode très facilement et très précisément.

Par exemple, si on instrumente RechercherTousLesCandidats de la sorte : 

procedure TSudokuNaif0.RechercherTousLesCandidats;
var
  x, y : integer;
  t0 : int64;
begin
  GenericLogger.TraceBegin(EVENT_START, 'RechercherTousLesCandidats', t0);
  try
    inc(NbResoudre);
    for x := 0 to LARGEUR-1 do
    begin
      for y := 0 to HAUTEUR-1 do
      begin
        if FGrille[x, y].Valeur<>CELLULE_VIDE
        then continue;

        CandidatsPossibles(x, y); // On recherche les coups possible de la cellule.
      end;
    end;
  finally
    GenericLogger.TraceEnd(EVENT_END, 'RechercherTousLesCandidats', t0);
  end;
end;
On fait la même chose sur les principales méthodes de notre programme de résolution, et on obtient le résultat suivant :

On voit alors qu'entre deux occurrences de Resoudre, il s'écoule environ 60 microsecondes, dont 47 sur RechercherTousLesCandidats, et 7 sur RechercherMinimumCandidat.

Devant de tels résultats, on sait immédiatement qu'il faut qu'on s'occupe de RechercherTousLesCandidats en premier.


II-B. Optimisation de l'algorithme naïf 0


II-B-1. RechercherTousLesCandidats

Commençons par s'intéresser à l'algorithme utilisé :

  • Pour chaque cellule de la grille, on teste tous les candidats possibles. Donc potentiellement, on va exécuter 81 fois le traitement suivant.
  • Pour chaque valeur possible de VALEUR_MIN à VALEUR_MAX, on vérifie si la valeur n'est pas déjà présente sur la ligne (9 tests), sur la colonne (9 tests), et dans la région (9 tests).
Donc au final, on effectue (9 + 9 + 9)*9*81 = 19683 tests. Pour effectuer ces tests, on doit gérer 7 boucles avec différentes imbrications. Ca fait déjà beaucoup de tests non ?

On devra bien passer sur chaque cellule pour rechercher tous ses candidats possibles. En revanche, on peut peut-être améliorer la recherche des candidats d'une seule cellule.

Dans CandidatsPossibles, on regarde si chaque chiffre peut être candidat. Pour cela, on doit tester la ligne, colonne, et region avec les boucles, et nombreux tests dont on a déjà parlés. Mais si on réfléchit un peu, on se rend vite compte qu'on pourrait très bien tester tous les candidats d'un coup !

Au lieu de se demander quels sont les candidats possibles, il suffit de rechercher les candidats interdits. Et là c'est très simple : Les candidats interdits sont les valeurs déjà placées sur la ligne, colonne, région. Il suffit de parcourir la ligne, colonne, region une seule fois, en excluant les valeurs trouvées de la liste des candidats.

De plus, on peut s'économiser une boucle en testant la ligne et la colonne dans la même boucle puisque la grille est carrée !

On divisera ainsi par 9 le nombre de tests à réaliser. RechercherTousLesCandidats devrait alors pouvoir approcher les 5 microsecondes.

Voyons ça tout de suite, si on écrit CandidatsPossibles de la façon suivante : 

procedure TSudokuNaif1.CandidatsPossibles(x, y : integer);
var
  Candidat : integer;
  i,j : integer;
  x1, y1 : integer;
begin
  // Par défaut, tous les coups sont possibles.
  fillchar(FGrille[x, y].FlgCandidats, sizeof(FGrille[x, y].FlgCandidats), 1);

  // On interdit les valeurs déjà utilisées en ligne ou en colonne.
  for i := 0 to LARGEUR-1 do
  begin
    FGrille[x, y].FlgCandidats[FGrille[i, y].Valeur] := false;
    FGrille[x, y].FlgCandidats[FGrille[x, i].Valeur] := false;
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      FGrille[x, y].FlgCandidats[FGrille[i,j].Valeur] := false;
    end;
  end;
end;
Cette fois, les temps d'exécution de RechercherTousLesCandidats passent à 8 microsecondes. Ce n'est pas encore aussi bon que ce qu'on pouvait espérer, mais c'est déjà un gain très important !

De plus, si on regarde le code, on voit qu'on passe notre temps à calculer FGrille[x, y], c'est-à-dire l'adresse de la cellule pour laquelle on détermine les candidats. On peut économiser ce calcul en définissant un pointeur sur la cellule en question. Ca donne le résultat suivant : 

procedure TSudokuNaif1.CandidatsPossibles(x, y : integer);
var
  Candidat : integer;
  i,j : integer;
  x1, y1 : integer;
  Cellule : PCellule;
begin
  // Par défaut, tous les coups sont possibles.
  Cellule := @FGrille[x, y];

  fillchar(Cellule.FlgCandidats, sizeof(Cellule.FlgCandidats), 1);

  // On interdit les valeurs déjà utilisées en ligne ou en colonne.
  for i := 0 to LARGEUR-1 do
  begin
    Cellule.FlgCandidats[FGrille[i, y].Valeur] := false;
    Cellule.FlgCandidats[FGrille[x, i].Valeur] := false;
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      Cellule.FlgCandidats[FGrille[i,j].Valeur] := false;
    end;
  end;
end;
Cette fois, RechercherTousLesCandidats passe à 6 microsecondes, ce qui rend la méthode plus rapide que RechercherMinimumCandidats, et du même coup, le temps de résolution de AI-Escargot descend à 1 ms (Algorithme naïf 1).

En toute rigueur, ce code contient un bug ! En effet, les bornes de FlgCandidats varient de VALEUR_MIN à VALEUR_MAX, c'est-à-dire de 1 à 9. Or avec notre code, on va exécuter à un moment ou à un autre : FlgCandidats[0] := false, et provoquer ainsi un écrasement mémoire quelque part (ou une violation d'accès...). On peut contourner le problème de différentes façons. Le pire serait de tester le cas de la valeur 0. En effet, on ajouterait un test pour chaque calcule, ce qui doublerait les temps.

On peut se contenter d'agrandir le tableau pour inclure la borne 0. De toute façon, plus tard, on verra comment faire complètement différemment, donc on oubliera vite ce problème.


II-C. Optimisation de l'algorithme naïf 1

Peut-on encore améliorer RechercherTousLesCandidats ? Ca commence à devenir plus difficile, mais on a toujours quelques axes de progrès. Dans notre implémentation, pour chaque cellule, on va tester la ligne, la colonne et la région, soit 9 + 9 +9 = 27 Tests. Mais si on fait l'intersection de tout ça, on voit vite qu'on va tester certaines cellules plusieurs fois : Une fois qu'on a testé la ligne, on a déjà testé une cellule de la colonne. Donc il ne devrait rester que 8 cellules à tester. De même lorsqu'on a été la ligne et la colonne, on a déjà traité 3 + 2 = 5 cellules. Donc il ne devrait rester que 4 cellules à tester. Au final, on ne devrait avoir à tester que 9 + 8 + 4 = 21 cellules. Et même, on n'a pas besoin de tester la cellule pour laquelle on calcule les candidats. Donc on doit pouvoir s'en sortir avec seulement 20 tests au lieu de 27. Ainsi, on a déjà une marge de progression de 26%.

Reste à voir comment organiser le code pour n'effectuer que ces 20 tests. On pourrait s'en sortir facilement, en passant par une liste pré-calculée qui nous indiquerait cellule par cellule, la liste des 20 autres cellules à tester ! En plus, on remplacerait ainsi la plupart des boucles par une seule.

Cependant, on va terriblement complexifier le code, pour un gain maximal de l'ordre de 26% sur RechercherTousLesCandidats. Ne pourrait-on pas faire plus simple, tout en obtenant des gains encore bien supérieurs ?

J'ai l'habitude de dire : "Le meilleure moyen pour réduire le temps d'exécution d'un traitement, c'est tout simplement de ne pas l'exécuter !" (ça marche à toutes les sauces, quel que soit le traitement). Ne rigoler pas ! C'est très sérieux.

Concrètement, ça veut dire : "Est-on réellement obligé d'appeler RechercherTousLesCandidats à chaque occurrence de Resoudre ?" Evidemment, si je pose la question, c'est que la réponse est non.

Entre deux appels de Resoudre, on a fait évoluer la grille en remplissant une seule cellule. Or lorsqu'on place une valeur dans une cellule, on sait très bien que cela va seulement impacter les candidats des cellules vides de la même ligne, colonne et region. Donc chaque fois qu'on place une valeur dans une cellule, au lieu de rechercher les candidats possibles pour toute la grille, on peut se contenter d'interdire la valeur qu'on vient de placer des candidats de la ligne, colonne et région.

Le traitement sera ainsi similaire à CandidatsPossibles. Sauf qu'au lieu de l'exécuter 81 fois à chaque appel de Resoudre, on ne l'exécutera plus qu'une seule et unique fois ! De cette façon, on pourra aller jusqu'à diviser les 6 microsecondes de RechercherTousLesCandidats par 81 !

Nous écrivons la méthode InterdireCandidats de la façon suivante : 

procedure TSudokuNaif2.InterdireCandidats(x, y, valeur : integer);
var
  i,j : integer;
  x1, y1 : integer;
begin
  // On interdit la valeur fournie en paramètre
  for i := 0 to LARGEUR-1 do
  begin
    FGrille[i, y].FlgCandidats[valeur] := false;
    FGrille[x, i].FlgCandidats[Valeur] := false;
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      FGrille[i,j].FlgCandidats[valeur] := false;
    end;
  end;
end;
Puis, nous devons modifier Resoudre pour ne plus appeler RechercherTousLesCandidats : 

function TSudokuNaif2.Resoudre(NbMaxSolution : integer) : boolean;
var
  x, y : integer;
  n : integer;
  old : array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
  t0 : int64;
begin
  result := true;

  // On recherche la première cellule avec le moins de candidats possibles.
  RechercherMinimumCandidat(x, y);
  if (x=-1) and (y=-1)
  then begin
    result := true; // La résolution est terminée !
    MemoriserSolution; // On mémorise la solution trouvée.
  end
  else begin
    if (x=-2) and (y=-2)
    then result := false // La grille n'a pas de solutions !
    else begin
      // On commence par sauvegarder la grille pour pouvoir faire un retour arrière par la suite.
      move(FGrille, old, sizeof(FGrille));

      for n := VALEUR_MIN to VALEUR_MAX do
      begin
        if FGrille[x, y].FlgCandidats[n]
        then begin
          // On essaie la résolution avec le candidat n
          FGrille[x, y].Valeur := n;
          InterdireCandidats(x, y, n); // On vient de placer une valeur, il faut appliquer
          // la modification des candidats possibles !

          // On continue recursivement.
          result := Resoudre(nbMaxSolution);

          // Si la grille a été résolue et qu'on a atteind le nombre maximum de solutions autorisé
          // on doit arrêter la recherche. Ca évite de boucler trop longtemps pour les grilles avec un
          // très grand nombre de solutions.
          if result and (ListeSolution.Count >= NbMaxSolution)
          then exit;

          // On vient de traiter le candidat n. On restaure la grille dans son état initial pour
          // continuer avec le candidat suivant.
          move(old, FGrille, sizeof(FGrille));
        end;
      end;
    end;
  end;
end;
Cependant, n'oublions pas que pour que cela fonctionne, il faudra malgré tout appeler RechercherTousLesCandidats une première fois, avant d'appeler Resoudre.

A présent, AI-Escargot est résolu en 0,567 ms !

Si on se réfère à notre profil d'exécution initial, on avait 60 microsecondes entre deux occurrences de Resoudre, dont 47 pour RechercherTousLesCandidats. Maintenant, les 47 microsecondes sont devenues négligeables !


II-D. Optimisation de l'algorithme naïf 2


II-D-1. RechercherMinimumCandidat

Si on veut continuer l'optimisation, il faut se tourner vers RechercherMinimumCandidat.

Cette méthode parcoure les 81 cellules et pour chaque cellule, on boucle pour compter les candidats. Puis pour chaque nombre de candidats trouvé, on mémorise la position correspondante.

Ainsi, on effectue 81*9 = 729 opérations pour compter les candidats et localiser l'emplacement de chaque cellule par nombre de candidats. C'est déjà énorme !

Si on veut appliquer la même technique d'optimisation que pour RechercherTousLesCandidats, on doit essayer :

  1. De réduire le nombre d'opérations
  2. De ne plus appeler RechercherMinimumCandidat (ou au moins, pas aussi souvent).
Alors commençons, comment réduire le nombre d'opérations ?

On doit passer sur chaque cellule pour compter les candidats. On a déjà fait l'optimisation qui consiste à sauter les cellules qui ne sont pas vides. De même, dès qu'on tombe sur une cellule sans solution, on arrête immédiatement la recherche.

On pourrait réduire le nombre d'opération en gérant un index des cellules vides. C'est-à-dire avoir une liste qui nous dirait directement quelles sont les cellules déjà remplies, et celles qu'on doit tester. Cependant, il faudrait maintenir cette liste à jour. Ca gestion serait probablement plus coûteuse que le gain potentiel !

Non, la seule façon de réduire le nombre d'opérations serait de ne plus compter les candidats ! On pourrait par exemple renvoyer la première cellule vide. On diviserait par 9 le nombre d'opérations, et on n'aurait plus besoin de scanner toute la grille ! Ne rêvons pas, dans ce cas, Resoudre poserait beaucoup plus d'hypothèses, devrait faire plus de retour arrière et au final RechercherMinimumCandidat serait appelé beaucoup plus souvent ! Autant dire que tout l'algorithme s'effondrerait.

Tant pis, voyons plutôt comment ne plus appeler RechercherMinimumCandidat. Le rôle de cette méthode est d'indiquer à Resoudre si :

  • La grille est résolue.
  • On est dans une impasse.
  • Trouver la cellule qui, lorsqu'on posera une hypothèse aura la plus faible probabilité de conduire à une impasse.
On voit tout de suite qu'on ne peut pas s'éviter d'appeler RechercherMinimumCandidat à chaque occurrence de Resoudre, puisque c'est cette méthode qui permet d'arrêter la récursion.

Alors que faire ? Comment limiter le nombre d'appels malgré tout ? Si on ne peut pas réduire le nombre d'appels à RechercherMinimumCandidat par appel à Resoudre, il faut réduire le nombre d'appels à Resoudre !

C'est tellement évident, qu'on aurait pu commencer tout de suite par là.

En fait actuellement on appelle Resoudre pour chaque cellule à remplir. Mais on ne tire pas parti du cas particulier des cellules évidentes !

En effet, si lors de la recherche dans RechercherMinimumCandidat on trouve une cellule qui ne possède qu'un seul et unique candidat, on sait qu'on peut remplir la cellule avec cette valeur sans se tromper. Si ce n'était pas la bonne valeur, ça signifie que l'erreur a été commise plus tôt par résoudre.

Finalement, en un seul scan de RechercherMinimumCandidat, on pourrait très bien avancer de plusieurs cellules dans la résolution, tout en identifiant la prochaine cellule à jouer pour Resoudre.

Il faut cependant réfléchir à quelques cas un peu spéciaux qui peuvent se présenter :

Ici, on a deux cellules évidentes pour lesquels on va vouloir remplir la cellule avec un 4. En réalité, on se trouve dans une impasse car une fois qu'on a remplit la première cellule, la deuxième n'a plus de solution ! Mais si on remplit toutes les cellules évidentes dans RechercherMinimumCandidat, on risque de faire l'erreur de mettre un 4 dans les deux cellules, ce qui conduirait à fournir des grilles invalident en guise de solution.

Si on avait gardé le fonctionnement où on appelait RechercherTousLesCandidats a chaque appel de Resoudre, on peut être sûr que ce cas nous aurait posé problème.

Cependant maintenant avec InterdireCandidats le fait de remplir la première cellule va nous conduire à interdire le 4 de la deuxième cellule, et on détectera qu'il n'y a pas de solutions !

On peut également avoir la situation suivante :

Cette fois, le fait de remplir la première cellule avec un 4, va faire apparaitre une nouvelle cellule évidente à 8. Une fois encore, grâce à InterdireCandidats, on va pouvoir jouer les deux cellules en un seul scan de la grille !

Mais que faire dans le cas suivant :

On va remplir la cellule avec la valeur 8, ce qui va faire apparaître une nouvelle cellule évidente à 4. Cependant, RechercherMinimumCandidat sera déjà passé sur cette cellule va renvoyer une cellule avec 2 candidats à Resoudre, alors qu'il existe pourtant une cellule évidente ! On risque donc de perdre du temps inutilement.

On pourrait recommencer le scan de la grille tant qu'on trouve des valeurs évidentes à jouer. Cependant, si on y réfléchit bien, ce cas de figure est qu'en même peu probable. Si on recommence le scan à chaque fois qu'on a trouvé des cellules évidentes à remplir, on va doubler le temps de traitement pour rien la plupart du temps.

Donc finalement, même si RechercherMinimumCandidat ne retourne pas la meilleure cellule à jouer à Resoudre, la dégradation des performances ne sera pas si fréquente que cela. L'un dans l'autre, on va s'y retrouver.

Nous pouvons donc ré-écrire RechercherMinimumCandidat de la façon suivante : 

procedure TSudokuNaif3.RechercherMinimumCandidat(var x, y: integer);
var
  i, j : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[VALEUR_MIN..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  for j := 0 to HAUTEUR-1 do
  begin
    for i := 0 to LARGEUR-1 do
    begin
      Cellule := @FGrille[i, j];
      // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
      if Cellule.Valeur<>CELLULE_VIDE
      then continue;

      // A présent, on compte les candidats.
      nb := 0;
      for n := VALEUR_MIN to VALEUR_MAX do
      begin
        if (Cellule.FlgCandidats[n])
        then inc(nb);
      end;

      case nb of
      0: // La cellule n'a pas de solution. La grille est impossible !
        begin
          x := -2;
          y := -2;
          exit;
        end;
      1: // La cellule est évidente !
        begin
          // On joue la valeur
          for n := VALEUR_MIN to VALEUR_MAX do
          begin
            if (Cellule.FlgCandidats[n])
            then begin
              Cellule.Valeur := n;
              InterdireCandidats(i, j, n);
              break;
            end;
          end;
        end;
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := (i shl 8) or j;
          CoupTrouve[nb] := true;
        end;
      end;
      end;
    end;
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      x := (tbPossible[n] and $ff00) shr 8;
      y := tbpossible[n] and $ff;
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  x := -1;
  y := -1;
end;
A présent, si on relance la résolution, AI-Escargot est résolu en 0,1393 ms ! On vient tout simplement de diviser le temps résolution par 4.

Je pense que nous avons à présent fini avec les optimisations de l'algorithme.

Retenons le gain obtenu : On est passé de 6 ms à 0.140 ms. Soit un gain de 43 !

En optimisant l'algorithme de résolution pour limiter sa combinatoire, on a divisé par 43 les temps d'exécution.

C'est déjà une très bonne performance. Mais puisqu'on est dans le cadre d'un Défi peut-on encore faire mieux ?

Evidement, la réponse est oui ! Nous avons terminé avec les optimisations de l'algorithme (enfin pour l'instant). Nous pouvons passer aux optimisations purement techniques.


III. Optimisations techniques


III-A. Algorithme optimisé 0

Maintenant que nous avons optimisé l'algorithme, nous allons essayer d'accélérer encore le traitement en optimisant son implémentation.

Nous allons donc reprendre chaque méthode une par une, et regarder tout ce qu'on peut faire sur le plan technique afin d'économiser un maximum de cycles horloges.

Attention : Une petite mise ne garde s'impose. C'est lorsqu'on commence à entrer dans ce genre d'optimisations, que le code devient particulièrement illisible et difficile à maintenir. Il faut donc garder ses objectifs en tête en permanence, et faire attention à conserver un bon équilibre entre optimisation et lisibilité !

Si on regarde à nouveau le profil d'exécution de la résolution de la grille, on constate que RechercherMinimumCandidat occupe toujours 5 microsecondes et représente l'essentiel des temps de traitement.

Il faut donc encore qu'on commence par RechercherMinimumCandidat. Cette dernière se compose de 3 boucles imbriquées, dont les deux premières servent à parcourir un tableau à deux dimensions. On calcule l'adresse d'une cellule, puis on boucle à nouveau pour compter les candidats.

Je l'ai déjà dit, ça fait trois boucles, il y en a deux de trop ! On peut très facilement remplacer les deux premières par une seule : Au lieu d'avoir un tableau à double entrée, il suffit de travailler avec un tableau à une seule dimension. Mais ne serait-il pas intéressant de pouvoir compter les candidats de la cellule, sans avoir besoin de faire de boucle ? Le résultat pourrait être très intéressant.

Il faudrait que l'on puisse en une seule opération, reconnaitre la configuration des candidats autorisés, et en déduire le nombre de candidats de la cellule. Par exemple, avec une table pré-calculée. Il faudrait alors que l'on puisse utiliser FlgCandidats comme un index dans cette table.

Avec un tableau de boolean, ce n'est pas possible. Sauf à calculer un hash sur le tableau, mais ce calcul serait plus couteux que la boucle qu'on veut éviter. En revanche, ce serait possible si FlgCandidats était un masque de bits ! Dans ce cas, ça donnerait un index sur 9 bits, soit une table lookup de 512 valeurs.

Par contre, ça nécessite de revoir nos structures de données, et de changer pas mal de chose. Mais comme je pense que le jeu en vaut la chandelle, on va essayer tout de suite.

La grille de jeu était définie de la façon suivante : 

FGrille : array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
Avec : 

TCellule = record
  Valeur : integer;     // Valeur de la cellule
  IsRevelee : boolean; // indique si la cellule est revéllée : Sa valeur est fournie au départ.
  FlgCandidats : array[VALEUR_MIN..VALEUR_MAX] of boolean; // désigne les marques définies par le joueur
end;
Si on réfléchit bien, IsRevelee n'intervient pas dans la résolution de la grille. Ce champ ne sert que pour sa présentation et pour bloquer la saisie manuelle. On peut lui faire un tableau dédié.

On veut stocker FlgCandidats sur un champ de 9 bits. Comme on doit travailler sur des multiples de 8, on va devoir prendre 16 bits, soit un word.

Valeur est stockée dans un integer, soit 4 octets. Un byte serait suffisant.

Cependant, pour garder l'alignement des variables en mémoire, il est préférable que la taille de TCellule soit un multiple de 4. Il faudrait donc ajouter un octet de calage pour rester à 4.

Donc autant garder IsRevelee dans la structure.

Finalement, notre nouvelle définition de TCellule devient la suivante : 

TCellule = record
  Valeur : byte;     // Valeur de la cellule
  IsRevelee : boolean; // indique si la cellule est revéllée : Sa valeur est fournie au départ.
  FlgCandidats : word; // désigne les marques définies par le joueur
end;
Nous devons alors réécrire CandidatsPossibles et InterdireCandidats de la façon suivante : 

procedure TSudokuOptimise0.InterdireCandidats(x, y, valeur : integer);
var
  i,j : integer;
  x1, y1 : integer;
  masque : word;
begin
  masque := MasqueCandidats[valeur];
  // On interdit la valeur fournie en paramètre
  for i := 0 to LARGEUR-1 do
  begin
    FGrille[i, y].FlgCandidats := FGrille[i, y].FlgCandidats and masque;
    FGrille[x, i].FlgCandidats := FGrille[x, i].FlgCandidats and masque;
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      FGrille[i,j].FlgCandidats := FGrille[i,j].FlgCandidats and masque;
    end;
  end;
end;

procedure TSudokuOptimise0.CandidatsPossibles(x, y: integer);
var
  i,j : integer;
  x1, y1 : integer;
  Cellule : PCellule;
begin
  // Par défaut, tous les coups sont possibles.
  Cellule := @FGrille[x, y];

  Cellule.FlgCandidats := TOUS_LES_CANDIDATS;

  // On interdit les valeurs déjà utilisées en ligne ou en colonne.
  for i := 0 to LARGEUR-1 do
  begin
    Cellule.FlgCandidats := Cellule.FlgCandidats and
      MasqueCandidats[FGrille[i, y].Valeur] and
      MasqueCandidats[FGrille[x, i].Valeur];
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      Cellule.FlgCandidats := Cellule.FlgCandidats and MasqueCandidats[FGrille[i,j].Valeur];
    end;
  end;
end;
FlgCandidat est maintenant utilisé au niveau binaire. Le bit de poids faible indique si VALEUR_MIN est un candidat possible, le bit suivant représente VALEUR_MIN+1… Pour positionner un bit indépendamment des autres, on doit effectuer des OR ou des AND arithmétiques sur le champ de bits. Il suffit alors d'utiliser le masque approprié.

CandidatsPossibles et InterdireCandidats doivent toujours effacer un bit dans le champ de bit. Pour cela, on fait un AND arithmétique avec un masque pour lequel on positionne à 1 les bits qu'on ne veut pas modifier et à 0 ceux qu'on veut effacer.

Pour calculer le masque pour effacer le candidat n, on doit calculer : 

MasqueOR := 1 shl (n-1);
Ceci retourne une valeur dont le bit de poids n-1 est à 1. Comme on veut exactement l'inverse pour faire un AND, il suffit d'enchaîner avec un NOT. 

masqueAND := not (1 shl (n-1));
Pour éviter que le calcul du masque lui-même ne ralentisse le traitement (3 opérations), on passe par une table pré-calculée, définie en constante (1 seule opération) : 

const
  MasqueCandidats : array[0..16] of cardinal =
    (cardinal(not 0),
     cardinal(not (1 shl  0)),
     cardinal(not (1 shl  1)),
     cardinal(not (1 shl  2)),
     cardinal(not (1 shl  3)),
     cardinal(not (1 shl  4)),
     cardinal(not (1 shl  5)),
     cardinal(not (1 shl  6)),
     cardinal(not (1 shl  7)),
     cardinal(not (1 shl  8)),
     cardinal(not (1 shl  9)),
     cardinal(not (1 shl 10)),
     cardinal(not (1 shl 11)),
     cardinal(not (1 shl 12)),
     cardinal(not (1 shl 13)),
     cardinal(not (1 shl 14)),
     cardinal(not (1 shl 15)));
De cette façon, RechercherMinimumCandidat va pouvoir s'affranchir de compter les candidats en faisant un simple lookup dans une autre table pré-calculée : 

procedure TSudokuOptimise0.RechercherMinimumCandidat(var x, y: integer);
var
  i, j : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[0..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  for j := 0 to HAUTEUR-1 do
  begin
    for i := 0 to LARGEUR-1 do
    begin
      Cellule := @FGrille[i, j];
      // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
      if Cellule.Valeur<>CELLULE_VIDE
      then continue;

      // A présent, on compte les candidats.
      nb := NombreCandidats[Cellule.FlgCandidats];
      case nb of
      0: // La cellule n'a pas de solution. La grille est impossible !
        begin
          x := -2;
          y := -2;
          exit;
        end;
      1: // La cellule est évidente !
        begin
          // On joue la valeur
          n :=  ValeurEvidente[Cellule.FlgCandidats];
          Cellule.Valeur := n;
          InterdireCandidats(i, j, n);
        end;
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := (i shl 8) or j;
          CoupTrouve[nb] := true;
        end;
      end;
      end;
    end;
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      x := (tbPossible[n] and $ff00) shr 8;
      y := tbpossible[n] and $ff;
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  x := -1;
  y := -1;
end;
Maintenant, on résout AI-Escargot en 0.0691 ms (au lieu de 0.140) (Algorithme optimisé 0). On a divisé le temps de résolution par deux !


III-B. Algorithme optimisé 1

Si on veut continuer à améliorer les performances, il faut optimiser encore RechercherMinimumCandidat. On a deux boucles imbriquées qui permettent de parcourir tous les éléments de la grille. Puis pour chaque élément, on calcule l'adresse de la cellule à tester.

On peut essayer de simplifier tout ça en traitant le tableau séquentiellement, et en utilisant l'arithméthique des pointeurs pour ne plus avoir besoin de calculer l'adresse d'une cellule.

Ca donne le résultat suivant : 

procedure TSudokuOptimise1.RechercherMinimumCandidat(var x, y: integer);
var
  i, j : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[0..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  Cellule := @FGrille[0, 0];
  for i := 0 to LARGEUR*HAUTEUR-1 do
  begin
    // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
    if Cellule.Valeur=CELLULE_VIDE
    then begin
      // A présent, on compte les candidats.
      nb := NombreCandidats[Cellule.FlgCandidats];

      case nb of
      0: // La cellule n'a pas de solution. La grille est impossible !
        begin
          x := -2;
          y := -2;
          exit;
        end;
      1: // La cellule est évidente !
        begin
          // On joue la valeur
          n :=  ValeurEvidente[Cellule.FlgCandidats];
          Cellule.Valeur := n;
          InterdireCandidats(i div LARGEUR, i mod LARGEUR, n);
        end;
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := i;
          CoupTrouve[nb] := true;
        end;
      end;
      end;
    end;
    inc(cardinal(Cellule), sizeof(TCellule));
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      x := tbPossible[n] div LARGEUR;
      y := tbpossible[n] mod LARGEUR;
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  x := -1;
  y := -1;
end;
Grâce à cette dernière optimisation, le temps de résolution de AI-Escargot passe à 0.7424 ms.

Aïe, nous étions à 0.0691 ms et on se retrouve à 0.7424 ms. Non seulement on n'a pas obtenu le résultat attendu, mais en plus c'est une véritable catastrophe. C'est tellement catastrophique que le seul fait de passer à l'arithmétique des pointeurs et supprimer un for ne peut pas expliquer un tel écart !


III-C. Algorithme optimisé 2

Alors que ce passe-t-il ? Si on fait attention, avant nous avions une première boucle pour parcourir les lignes, puis une deuxième pour parcourir les colonnes. La grille était donc traitée dans lorsque : De gauche à droite, puis de haut en bas.

A présent, on se déplace de cellules en cellules, en passant à la cellule qui se trouve immédiatement après la précédente en mémoire vive. Or si on reprend la définition du tableau, on a : 

FGrille : array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
Ce qui revient à dire : 

FGrille : array[0..LARGEUR-1] of array[0..HAUTEUR-1] of TCellule;
Autrement dit, l'organisation du tableau en mémoire vive n'est pas un ensemble de lignes de cellules, mais un ensemble de colonnes de cellules. Lorsqu'on passe à l'élément suivant en incrémentant le pointeur, on ne se déplace pas sur la cellule de la colonne suivante, mais sur la cellule de la ligne suivante !

Voilà pourquoi le temps de résolution a changé de façon aussi drastique. Si on veut pouvoir comparer notre arithmétique des pointeurs avec la solution précédente, il faut qu'on conserve le même ordre de parcours des cellules. Si on veut conserver une seule boucle for ainsi que l'arithmétique des pointeurs, il va falloir qu'on passe à nouveau par une table pré-calculée intermédiaire qui nous indiquera l'ordre de parcours des cellules.

Ca donne le résultat suivant : 

procedure TSudokuOptimise2.RechercherMinimumCandidat(var x, y: integer);
type
  TbCellule = array[0..LARGEUR*HAUTEUR-1] of TCellule;
var
  i : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[0..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
  ptrCellNo : ^integer;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  ptrCellNo := @ParcoursCellNr[0];
  for i := 0 to LARGEUR*HAUTEUR-1 do
  begin
    Cellule := @tbCellule(FGrille)[ptrCellNo^];
    // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
    if Cellule.Valeur=CELLULE_VIDE
    then begin
      // A présent, on compte les candidats.
      nb := NombreCandidats[Cellule.FlgCandidats];

      case nb of
      0: // La cellule n'a pas de solution. La grille est impossible !
        begin
          x := -2;
          y := -2;
          exit;
        end;
      1: // La cellule est évidente !
        begin
          // On joue la valeur
          n :=  ValeurEvidente[Cellule.FlgCandidats];
          Cellule.Valeur := n;
          InterdireCandidats(ptrCellNo^ div HAUTEUR, ptrCellNo^ mod HAUTEUR, n);
        end;
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := ptrCellNo^;
          CoupTrouve[nb] := true;
        end;
      end;
      end;
    end;
    inc(cardinal(ptrCellNo), 4);
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      x := tbPossible[n] div HAUTEUR;
      y := tbpossible[n] mod HAUTEUR;
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  x := -1;
  y := -1;
end;
Avec ParcoursCellNr définit de la façon suivante : 

var   ParcoursCellNr : array[0..81] of integer;
…
  n := 0;
  for j := 0 to HAUTEUR-1 do
  begin
    for i := 0 to LARGEUR-1 do
    begin
      ParcoursCellNr[n] := i*HAUTEUR + j;
      inc(n);
    end;
  end;
Cette fois, le temps de résolution passe à 0.0670 ms au lieu de 0.0691 ms. Le gain est minime mais représente quand même 3%.


III-D. Algorithme optimisé 3

A présent, il nous reste à essayer de faire la même chose sur InterdireCandidats. Tout d'abord passons l'arithmétique des pointeurs : 

procedure TSudokuOptimise.InterdireCandidats(x, y, valeur : integer);
var
  i,j : integer;
  x1, y1 : integer;
  masque : word;
  CelluleLigne : pointer;
  CelluleColonne : pointer;
  CelluleRegion : pointer;
begin
  masque := MasqueCandidats[valeur];
  // On interdit la valeur fournie en paramètre
  CelluleLigne := @(FGrille[0, y].FlgCandidats);
  CelluleColonne := @(FGrille[x, 0].FlgCandidats);

  for i := 0 to LARGEUR-1 do
  begin
    word(CelluleLigne^) := word(CelluleLigne^) and masque;
    word(CelluleColonne^) := word(CelluleColonne^) and masque;
    inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
    inc(cardinal(CelluleColonne), sizeof(TCellule));
  end;

  // Et on recommence pour la région
  x1 := (x div LGBLOC)*LGBLOC;
  y1 := (y div HTBLOC)*HTBLOC;
  CelluleRegion := @(FGrille[x1,y1].FlgCandidats);
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      word(CelluleRegion^) := word(CelluleRegion^) and masque;
      inc(cardinal(CelluleRegion), sizeof(TCellule));
    end;
    inc(cardinal(CelluleRegion), sizeof(TCellule)*(HAUTEUR-HTBLOC));
  end;
end;
Maintenant, on résoud AI-Escargot en 0.0538 ms au lieu de 0.0670 ms. Soit un gain de 20 %.


III-E. Algorithme optimisé 4

Peut-on encore améliorer les résultats ?

Evidemment, le calcul des coordonnées de la région à tester fait appel à deux divisions ! Or la division est une opération coûteuse pour le processeur. On peut très bien les supprimer en passant par une table pré-calculée ! 

procedure TSudokuOptimise4.InterdireCandidats(x, y, valeur : integer);
var
  i,j : integer;
  x1, y1 : integer;
  masque : word;
  CelluleLigne : pointer;
  CelluleColonne : pointer;
  CelluleRegion : pointer;
begin
  masque := MasqueCandidats[valeur];
  // On interdit la valeur fournie en paramètre
  CelluleLigne := @(FGrille[0, y].FlgCandidats);
  CelluleColonne := @(FGrille[x, 0].FlgCandidats);

  for i := 0 to LARGEUR-1 do
  begin
    word(CelluleLigne^) := word(CelluleLigne^) and masque;
    word(CelluleColonne^) := word(CelluleColonne^) and masque;
    inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
    inc(cardinal(CelluleColonne), sizeof(TCellule));
  end;

  // Et on recommence pour la région
  x1 := RegionX[x];
  y1 := RegionY[y];
  CelluleRegion := @(FGrille[x1,y1].FlgCandidats);
  for i := x1 to x1 +LGBLOC-1 do
  begin
    for j := y1 to y1+HTBLOC-1 do
    begin
      word(CelluleRegion^) := word(CelluleRegion^) and masque;
      inc(cardinal(CelluleRegion), sizeof(TCellule));
    end;
    inc(cardinal(CelluleRegion), sizeof(TCellule)*(HAUTEUR-HTBLOC));
  end;
end;
Le temps de résolution de AI-Escargot passe alors à 0.0512 ms au lieu de 0.0538 ms. D'où un gain de 5%.


III-F. Algorithme optimisé 5

Peut-on encore optimiser cette méthode ?

Evidemment, il suffit de supprimer les boucles. Pour cela c'est vraiment très simple, il suffit de les développer : 

procedure TSudokuOptimise5.InterdireCandidats(x, y, valeur : integer);
var
  i,j : integer;
  x1, y1 : integer;
  masque : word;
  CelluleLigne : pointer;
  CelluleColonne : pointer;
  CelluleRegion : pointer;
begin
  masque := MasqueCandidats[valeur];
  // On interdit la valeur fournie en paramètre
  CelluleLigne := @(FGrille[0, y].FlgCandidats);
  CelluleColonne := @(FGrille[x, 0].FlgCandidats);

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;
  inc(cardinal(CelluleLigne), HAUTEUR*sizeof(TCellule));
  inc(cardinal(CelluleColonne), sizeof(TCellule));

  word(CelluleLigne^) := word(CelluleLigne^) and masque;
  word(CelluleColonne^) := word(CelluleColonne^) and masque;

  x1 := RegionX[x];
  y1 := RegionY[y];
  CelluleRegion := @(FGrille[x1,y1].FlgCandidats);

  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));

  inc(cardinal(CelluleRegion), sizeof(TCellule)*(HAUTEUR-HTBLOC));

  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));

  inc(cardinal(CelluleRegion), sizeof(TCellule)*(HAUTEUR-HTBLOC));

  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
  inc(cardinal(CelluleRegion), sizeof(TCellule));
  word(CelluleRegion^) := word(CelluleRegion^) and masque;
end;
Je vous avais prévenus, le code commence à devenir complètement illisible !

Mais malgré tous, le temps de résolution descend alors à 0.0485 ms au lieu 0.0512 ms, soit encore un gain de 5%.


III-G. Algorithme optimisé 6

Peut-on encore améliorer les performances ?

Tout d'abord, on a également deux divisions qu'on peut supprimer dans RechercherMinimumCandidats en passant par des tables pré-calculées (le temps de résolution passe alors à 0.450 ms).

RechercherMinimumCandidats utilise deux paramètres de sorti : X et Y. On pourrait éviter d'utiliser ces paramètres. Il suffit que RechercherMinimumCandidats devienne une fonction qui retourne le numéro de la cellule au lieu de ses coordonnées.

Mais si on veut vraiment obtenir un gain significatif, il faudrait qu'on accélère la détection des impasses. En effet, l'algorithme ressemble beaucoup à un brute force qui énumère toutes les combinaisons possibles. La plupart du temps, il va donc énumérer des combinaisons qui conduisent à une impasse. On ira donc d'autant plus vite qu'on détectera l'impasse rapidement et qu'on pourra alors arrêter la rechercher.

Actuellement, on teste une possibilité, on remplit une case, puis ce n'est que lors de l'itération suivante qu'on détectera si la grille possède une cellule sans solution !

Il serait intéressant de détecter l'existence de ces cases sans solutions au plus tôt, c'est-à-dire au moment ou on interdit le dernier candidat. Autrement dit, il faudrait que InterdireCandidats nous dises si la cellule qu'on vient de remplir a eut pour effet de définir une cellule sans solution !

Pour cela chaque fois qu'InterdireCandidats modifie le FlgCandidats d'une cellule, elle doit ensuite tester si les flags vaut 0. Pour chaque cellule testée, on devrait écrire un code du genre : 

tbCellule(CelluleLigne^)[0].FlgCandidats := tbCellule(CelluleLigne^)[0].FlgCandidats and masque;
if tbCellule(CelluleLigne^)[0].FlgCandidats<>0
then begin
  result := false;
  exit;
end;
Ceci répété 27 fois, une fois pour chaque cellule. Le code était illisible depuis qu'on a développé les boucles. Si on fait ça, il le deviendra encore plus (on multiplie le nombre de lignes de la méthode par 6). De plus le test en question va également dégrader les performances. Le AND avait un coût assez faible. Si on doit encore comparer le résultat obtenu avec 0, et faire un saut en fonction du résultat, il n'est pas sûr qu'on gagne grand-chose à la fin.

Heureusement, on peut s'en sortir assez facilement, avec une ligne de code en assembleur ! En effet le problème ici, c'est que le compilateur ne sait pas enchaîner les calculs en tirant parti du résultat suivant pour faire les sauts sans devoir refaire le test du 0.

Or dans le langage machine, lorsque le microprocesseur calcule le AND, il positionne en même temps un certain nombre d'indicateurs sur le résultat obtenu. En particulier, il positionne le flag ZF qui indique si le résultat vaut 0.

Ainsi, à l'issu de notre AND, il suffit d'effectuer directement un saut conditionnel si le flag ZF est positionné. Concrètement, nous ajoutons donc une instruction assembleur JZ, immédiatement après le calcul du AND.

Nous écrivons donc un code qui aura le même effet que si on écrivait : 

tbCellule(CelluleLigne^)[0].FlgCandidats := tbCellule(CelluleLigne^)[0].FlgCandidats and masque;
if tbCellule(CelluleLigne^)[0].FlgCandidats<>0
then goto fin;
Nous devons déclarer l'étiquette FIN. La nouvelle définition de InterdireCandidats devient : 

function TSudokuOptimise6.InterdireCandidats(x, y, valeur : integer) : boolean;
var
  x1, y1 : integer;
  masque : word;
  CelluleLigne : pointer;
  CelluleColonne : pointer;
  CelluleRegion : pointer;

label Fin;
begin
  masque := MasqueCandidats[valeur];
  // On interdit la valeur fournie en paramètre
  CelluleLigne := @(FGrille[0, y]);
  CelluleColonne := @(FGrille[x, 0]);

  tbCellule(CelluleLigne^)[0].FlgCandidats := tbCellule(CelluleLigne^)[0].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[0].FlgCandidats :=
    tbCellule(CelluleColonne^)[0].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[1].FlgCandidats :=
    tbCellule(CelluleColonne^)[1].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*2].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*2].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[2].FlgCandidats :=
    tbCellule(CelluleColonne^)[2].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*3].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*3].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[3].FlgCandidats :=
    tbCellule(CelluleColonne^)[3].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*4].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*4].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[4].FlgCandidats :=
    tbCellule(CelluleColonne^)[4].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*5].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*5].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[5].FlgCandidats :=
    tbCellule(CelluleColonne^)[5].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*6].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*6].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[6].FlgCandidats :=
    tbCellule(CelluleColonne^)[6].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*7].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*7].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[7].FlgCandidats :=
    tbCellule(CelluleColonne^)[7].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleLigne^)[HAUTEUR*8].FlgCandidats :=
    tbCellule(CelluleLigne^)[HAUTEUR*8].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleColonne^)[8].FlgCandidats :=
    tbCellule(CelluleColonne^)[8].FlgCandidats and masque;
  asm jz Fin end;

  x1 := RegionX[x];
  y1 := RegionY[y];

  CelluleRegion := @(FGrille[x1,y1]);
  tbCellule(CelluleRegion^)[0].FlgCandidats :=
    tbCellule(CelluleRegion^)[0].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[1].FlgCandidats :=
    tbCellule(CelluleRegion^)[1].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[2].FlgCandidats :=
    tbCellule(CelluleRegion^)[2].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR + 0].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR + 0].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR + 1].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR + 1].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR + 2].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR + 2].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR*2 + 0].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR*2 + 0].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR*2 + 1].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR*2 + 1].FlgCandidats and masque;
  asm jz Fin end;

  tbCellule(CelluleRegion^)[HAUTEUR*2 + 2].FlgCandidats :=
    tbCellule(CelluleRegion^)[HAUTEUR*2 + 2].FlgCandidats and masque;
  asm jz Fin end;
  
  result := true;
  exit;
fin:
  result := false;
end;
Il faut également modifier RechercherMinimumCandidats pour tenir compte de la nouvelle définition de InterdireCandidats. 

TSudokuOptimise6.RechercherMinimumCandidat : integer;
var
  i : integer;
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[0..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
  ptrCellNo : ^integer;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  ptrCellNo := @ParcoursCellNr[0];
  while (ptrCellNo^>=0) do
  begin
    Cellule := @tbCellule(FGrille)[ptrCellNo^];
    // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
    if Cellule.Valeur=CELLULE_VIDE
    then begin
      // A présent, on compte les candidats.
      nb := NombreCandidats[Cellule.FlgCandidats];
      if nb = 1
      then begin
        // On joue la valeur
        n :=  ValeurEvidente[Cellule.FlgCandidats];
        Cellule.Valeur := n;
        Cellule.FlgCandidats := $FFFF;
        if not InterdireCandidats(tbX[ptrCellNo^], tbY[ptrCellNo^], n)
        then begin
          result := -2;
          exit;
        end;
      end
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := ptrCellNo^;
          CoupTrouve[nb] := true;
        end;
      end;
    end;
    inc(cardinal(ptrCellNo), 4);
  end;

  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      result := tbPossible[n];
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  result := -1;
end;
On remarquera au passage que lorsqu'on examine ne nombre de candidats d'une cellule, il n'est plus nécessaire de prévoir le cas à 0 puisque c'est InterdireCandidats qui nous ne dit directement.

FParcoursCellNr est un tableau de byte, initialisé dans RechercherTousLesCandidats de la façon suivante : 

procedure TSudokuOptimise6.RechercherTousLesCandidats;
var
  x, y : integer;
  nb : integer;
  Cellule : PCellule;
begin
  nb := 0;
  for y := 0 to HAUTEUR-1 do
  begin
    for x := 0 to LARGEUR-1 do
    begin
      Cellule := @FGrille[x, y];
      if Cellule.Valeur<>CELLULE_VIDE
      then begin
        Cellule.FlgCandidats := $FFFF;
      end
      else begin //continue;
        CandidatsPossibles(x, y); // On recherche les coups possible de la cellule.
        FParcoursCellNr[nb] := x*HAUTEUR + y;
        inc(nb);
      end;
    end;
  end;
  FParcoursCellNr[nb] := -1;
end;
A présent, le temps d'exécution passe à 0.0455 ms au lieu des 0.0485 ms, ce qui donne à nouveau un gain de 6%.


III-H. Algorithme optimisé 7

Peut-on encore améliorer les performances ?

On peut exploiter différentes pistes. Si on se souvient bien, lorsque nous parlions d'optimiser l'algorithme de RechercherMinimumCandidat, j'ai di qu'on pourrait optimiser le traitement en indexant les cases vides. En effet, à chaque appel de la méthode, on parcourt la totalité de la grille. Plus on avance dans la résolution, plus la grille se remplit, et donc plus on va passer du temps à tester des cellules qu'il faut finalement ignorer.

Nous n'avions pas retenu cette solution car son implémentation aurait été délicate et probablement trop couteuse en temps par rapport au gain potentiel.

Cependant à présent, nous ne parcourons plus cellules dans l'ordre des boucles, mais l'ordre qui nous est donné par le tableau ParcoursCellNr. Or on pourrait très bien imaginer de faire en sorte que ce tableau ne nous demande plus de passer sur une cellule déjà remplie une fois qu'elle a été définie. Ainsi, il suffit qu'on trouve une méthode simple pour mettre à jour ce tableau pour s'éviter de re-tester les cellules déjà définies.

En fait, la méthode à suivre est très simple : On teste la grille dans l'ordre des cellules indiqué par ParcoursCellNr. Si ce tableau indique une cellule déjà remplie, on saute la cellule. Il suffit qu'on dresse en parallèle la liste des cellules vides trouvées, puis qu'on mette ParcoursCellNr à jour en lui recopiant cette liste ! De cette façon, on ne testera plus les cellules non vides lors de l'itération suivante.

On peut même faire encore mieux : On avance plus vite dans la lecture des cellules à tester que dans l'écriture des cellules vides (on ne peut pas trouver plus de cellules vides que de cellules testées). Donc on peut utiliser le même tableau pour lire les cellules à tester et écrire les cellules vides trouvées. De cette façon, nous n'auront pas besoin de mettre à jours ParcoursCellNr à la fin.

Il faut cependant faire attention au cas des retours arrière dans la recherche des solutions. En effet, si on fait un retour arrière, il faut également effectuer ce retour arrière sur ParcoursCellNr.

Pour gérer cela efficacement, on va intercaler ParcoursCellNr directement dans la définition de la grille elle-même !

Rappelons-nous que dans la définition de TCellule, nous avions un octet : IsRevele qui aurait pu être sorti de la structure. C'est ce que nous allons faire pour remplacer IsRevele par un élément de ParcoursCellNr.

Ca donne le résultat suivant : 

type
  PShortint = ^Shortint;
  TCellule = record
    Valeur : byte;     // Valeur de la cellule
    cellNo : byte; // indique si la cellule est revéllée : Sa valeur est fournie au départ.
    FlgCandidats : word; // désigne les marques définies par le joueur
  end;
  TbCellule = array[0..LARGEUR*HAUTEUR-1] of TCellule;

  PCellule = ^TCellule;

  TSudokuOptimise7 = class(TSudokuBase)
  private
    // Définition de la grille de Sudoku
    FGrille : array[0..LARGEUR-1, 0..HAUTEUR-1] of TCellule;
    FVide : array[0..LARGEUR-1, 0..HAUTEUR-1] of boolean;
    FRevele : array[0..LARGEUR-1, 0..HAUTEUR-1] of boolean;
Nous devons alors reprendre RechercherMinimumCandidat pour mettre en œuvre la technique qu'on vient de présenter : 

function TSudokuOptimise7.RechercherMinimumCandidat : integer;
var
  TbPossible : array[VALEUR_MIN..VALEUR_MAX] of integer;
  CoupTrouve : array[0..VALEUR_MAX] of boolean;
  nb : integer;
  n : integer;
  Cellule : PCellule;
  ptrCellNo : PShortint;
  ptrCellNo2 : PShortint;
  CellNo : byte;
begin
  // Pour chaque cellule, on doit compter le nombre de candidats possibles, et renvoyer la première
  // cellule qui possède le moins de candidats.
  Fillchar(CoupTrouve, sizeof(CoupTrouve), 0);

  ptrCellNo := @(FGrille[0,0].CellNo);
  ptrCellNo2 := ptrCellNo;
  while (ptrCellNo^>=0) do
  begin
    CellNo := ptrCellNo^;
    Cellule := @tbCellule(FGrille)[CellNo];
    // Si la cellule n'est pas vide, on peut passer à la suivante immédiatement.
    if Cellule.Valeur=CELLULE_VIDE
    then begin
      ptrCellNo2^ := CellNo;
      inc(ptrCellNo2, 4);
      // A présent, on compte les candidats.
      nb := NombreCandidats[Cellule.FlgCandidats];
      if nb = 1
      then begin
        // On joue la valeur
        n :=  ValeurEvidente[Cellule.FlgCandidats];
        Cellule.Valeur := n;
        Cellule.FlgCandidats := $FFFF;
        if not InterdireCandidats(tbX[CellNo], tbY[CellNo], n)
        then begin
          result := -2;
          exit;
        end;
      end
      else begin
        if not CoupTrouve[nb]
        then begin
          // On vient de trouver la première cellule avec Nb candidats possibles.
          tbPossible[nb] := CellNo;
          CoupTrouve[nb] := true;
        end;
      end;
    end;
    inc(cardinal(ptrCellNo), 4);
  end;
  ptrCellNo2^ := -1;
  // A présent, on retourne la première cellule ayant le plus petit nombre de candidats.
  for n := VALEUR_MIN to VALEUR_MAX do
  begin
    if CoupTrouve[n]
    then begin
      result := tbPossible[n];
      exit;
    end;
  end;
  // Si on arrive ici, c'est qu'on n'a pas trouvé de cellule vide avec au moin un candidat possible.
  // Comme le cas de la grille sans solution a déjà été traité, c'est qu'il n'y a pas de cellule vide,
  // et donc que la grille est terminée !
  result := -1;
end;
Cependant, on doit également initialiser les valeurs de CellNo dans la grille pour le premier appel à RechercherMinimumCandidats. C'est ce que nous faisons dans RechercherTousLesCandidats. Et tant qu'à faire, autant en profiter pour éliminer directement les révélées de la liste des cellules à traiter : 

procedure TSudokuOptimise7.RechercherTousLesCandidats;
var
  x, y : integer;
  Cellule : PCellule;
  ptrCellNo : PShortint;
  n : integer;
  CellNo : integer;
begin
  ptrCellNo := @(FGrille[0,0].CellNo);
  n := 0;
  while (ParcoursCellNr[n]>=0) do
  begin
    CellNo := ParcoursCellNr[n];
    Cellule := @tbCellule(FGrille)[CellNo];
    if Cellule.Valeur=CELLULE_VIDE
    then begin
      ptrCellNo^ := CellNo;
      inc(cardinal(ptrCellNo), 4);
      CandidatsPossibles(tbX[CellNo], tbY[CellNo]); // On recherche les coups possible de la cellule.
    end
    else Cellule.FlgCandidats := $FFFF;
    inc(n);
  end;
  ptrCellNo^ := -1;
end;
Vous remarquerez qu'on se base toujours sur le tableau ParcoursCellNr initial. Ce dernier détermine l'ordre dans lequel on va parcourir les cellules pour RechercherMinimumCandidats. Ici, nous nous contentons de supprimer les cellules des révélées de la liste, tout en respectant l'ordre prédéfinit.

A présent, le temps de résolution descend à 0.0374 ms au lieu de 0.0455 ms, soit un gain de 18% !


IV. Algorithme final

Il reste encore un dernier élément simple sur lequel on peut essayer de jouer pour améliorer les performances. On a vu que le temps de résolution variait beaucoup selon l'ordre dans lequel on parcourt les cellules lors de la résolution.

Par exemple, lorsqu'on faisait le parcours dans le sens colonne/ligne on mettait 0.0691 ms. Lorsqu'on s'est retrouvé par erreur à faire le parcours dans le sens ligne/colonne, le temps est passé à 0.7424 ms. Cet ordre a été choisi de façon purement arbitraire.

Qui plus est, on a utilisé un ordre continu. Ce dernier a pour effet qu'on essaie la résolution en remplissant en premier lieu les cellules des lignes du haut. Chaque fois qu'on remplit une valeur, on pose de nouvelles contraintes sur la grille qui vont nous permettre d'éliminer des candidats. Cependant, il si on remplit toujours les cellules qui se trouvent dans la même zone, on définit finalement assez peu de contraintes. On élimine donc assez peu de candidats.

Imaginons à présent qu'au contraire, on choisisse un ordre de parcours aléatoire, qui essaierait de définir des contraintes réparties un peu partout dans la grille. On éliminerait davantage de candidats, ce qui réduirait la combinatoire et accélérerait considérablement les calculs !

A présent, tel que nous avons implémenté l'algorithme, cette technique est très simple à mettre en œuvre : Il suffit de pré-initialiser le tableau ParcoursCellNr avec cet ordre aléatoire. Par exemple, si on définit ParcoursCellNr de la façon suivante : 

var
  ParcoursCellNr : array[0..81] of integer=
  (  19, 22,  1, 28, 46, 55, 64, 72, 47,
     38, 36, 65, 74, 77, 27, 54, 18, 58,
     23, 59, 68, 24,  9, 25,  2, 11, 31,
     49, 67, 75,  4, 66, 39, 48,  3, 12,
     14, 32, 41, 42, 44, 71, 43, 70, 17,
     80, 15, 51, 60, 78, 52, 61, 35, 53,
     33,  7, 34,  8,  0, 45, 63, 10, 37,
     73, 20, 29, 56, 21, 30, 57, 13, 40,
     76,  5, 50,  6, 69, 16, 79, 26, 62,
     -1
  );
A présent la résolution s'effectue en 0.0135 ms ! au lieu de 0.0374 ms, soit un gain de 64%

Impressionnant non ?

En fait en réalité, je n'ai pas choisit cet ordre n'importe comment au hasard. Et je n'ai pas cherché uniquement à répartir les contraintes pendant la résolution : Si on reprend notre algorithme de résolution, il arrive un moment où il doit poser des hypothèses. A ce moment, il dresse la liste des cellules qui possèdent le moins de candidats, prends la première cellule trouvée dans l'ordre de parcours et choisi le premier candidat comme première hypothèse à essayer.

Et bien j'ai tout simplement suivi la résolution de AI-Escargot, cellule par cellule, et chaque fois que l'algorithme a dû poser une hypothèse, j'ai défini l'ordre de parcours des cellules de façon à ce que la première cellule testée, ait pour premier candidat la valeur qui correspond à la solution de la grille.

Autrement dit, j'ai fait en sorte que lorsqu'on essaie de résoudre AI-Escargot, la première hypothèse posée soit toujours la bonne !

Ainsi, la résolution de la grille ne fait jamais d'erreur, d'où le résultat optimal obtenu.

Ce qui est d'autant plus intéressant, c'est que cette "optimisation" n'est pas pénalisante pour la résolution des autres grilles. On a seulement "optimisé" le paramétrage de l'algorithme de résolution pour qu'il soit optimal sur cette grille.

Tout ça pour dire qu'il faut toujours se méfier des tests de performances. En effet, comme on vient de la voir, on peut très facilement tricher sur les tests pour obtenir de très bons résultats, sans que ça ne soit visible !


V. Conclusion

Nous venons de voir l'élaboration d'une première solution naïve pour résoudre une grille de Sudoku. Ainsi, nous avons commencer par coder la première solution qui nous est passée par la tête.

Cette première solution a pu être codée rapidement, mais était relativement lente, et résolvait AI-Escargot en 6 ms.

Dans un dexième temps, nous avons utilisé des outils d'analyse tel que ETW afin d'identifier le profil d'exécution du code et connaitre ainsi les éléments à opitmiser.

Nous avons réalisé deux types d'optimisations. Une première série d'optimisations a porté directement sur l'algorithme, la réduction de sa combinatoire, et donc de sa complexité. Nous avons ainsi ramené le temps de résolution de 6 ms à 0.140 ms, pratiquement sans perdre en lisibilité.

Puis les optimisations algorithmiques ont laissé la place aux optimisations purement techniques. Nous avons alors réduit le temps de résolution à 0.0374 ms, au prix d'une perte importante en lisibilité et pas mal d'efforts.

Ainsi, si les optimisations de l'algorithme ont permis de diviser les temps de traitement par 40 assez facilement, les optimisations techniques elles n'auront permis qu'un gain de 3,7.

Enfin, on se rappellera qu'il faut se méfier des tests de performances pures, effectués sur un jeu de données assez limité puisqu'on a également pu voir qu'il était facil de tricher avec l'algorithme final et AI-Escargot !

Téléchargez les sources de la solution complète



               Version PDF (Miroir)   Version hors-ligne (Miroir)

Valid XHTML 1.0 TransitionalValid CSS!

Les sources présentées sur cette page sont libres de droits et vous pouvez les utiliser à votre convenance. Par contre, la page de présentation constitue une œuvre intellectuelle protégée par les droits d'auteur. Copyright © 2009 Franck SORIANO. Aucune reproduction, même partielle, ne peut être faite de ce site ni de l'ensemble de son contenu : textes, documents, images, etc. sans l'autorisation expresse de l'auteur. Sinon vous encourez selon la loi jusqu'à trois ans de prison et jusqu'à 300 000 € de dommages et intérêts.